¿Que es y que estudia la geometría analítica?

La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería.
Lo novedoso de la geometría analítica es que representa las figuras geométricas mediante fórmulas del tipo
 , donde
, donde  es una función u otro tipo de expresión matemática.
es una función u otro tipo de expresión matemática.
Es muy importante conocer el plano cartesiano y los sistemas de coordenadas, para graficar un punto en el plano hay que saber que esta compuesto por dos números determinados , estas coordenadas se escriben así  y representan correspondientemente a la abscisa (distancia horizontal en el eje x) y ordenada (distancia vertical en el eje y).
y representan correspondientemente a la abscisa (distancia horizontal en el eje x) y ordenada (distancia vertical en el eje y).
 y representan correspondientemente a la abscisa (distancia horizontal en el eje x) y ordenada (distancia vertical en el eje y).
y representan correspondientemente a la abscisa (distancia horizontal en el eje x) y ordenada (distancia vertical en el eje y).
"A cada punto en un plano le corresponde un par ordenado de números y a cada par ordenado de números le corresponde un punto en un plano."
Las líneas y ciertas figuras geométricas se pueden expresar como ecuaciones y, a su vez, las ecuaciones pueden graficarse como líneas o figuras geométricas, en particular, las rectas pueden expresarse como ecuaciones polinómicas de primer grado y las circunferencias y el resto de cónicas como ecuaciones polinómicas de segundo grado
Sección cónica: el corte de la superficie de un cono da lugar a lo que se denomina sección cónica que son:
- La parábola
- La elipse
- la hipérbola
La parábola es el lugar geométrico de todos los puntos que de un punto fijo llamado foco y de una recta fija llamada generatriz,la parábola resulta de cortar un cono recto.
Una parábola cuyo eje de simetría sea paralelo al eje de abscisas se expresa mediante la ecuación:


Una elipse es la curva cerrada con dos ejes de simetría que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto de su eje de revolución.
Se representa mediante la ecuación:
Una hipérbola es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución tiene por expresión:




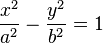
.png/220px-Hyperbola_(PSF).png)
No hay comentarios:
Publicar un comentario